Decoding Hidden Markov Model

Hidden Markov Model



An example of HMM.

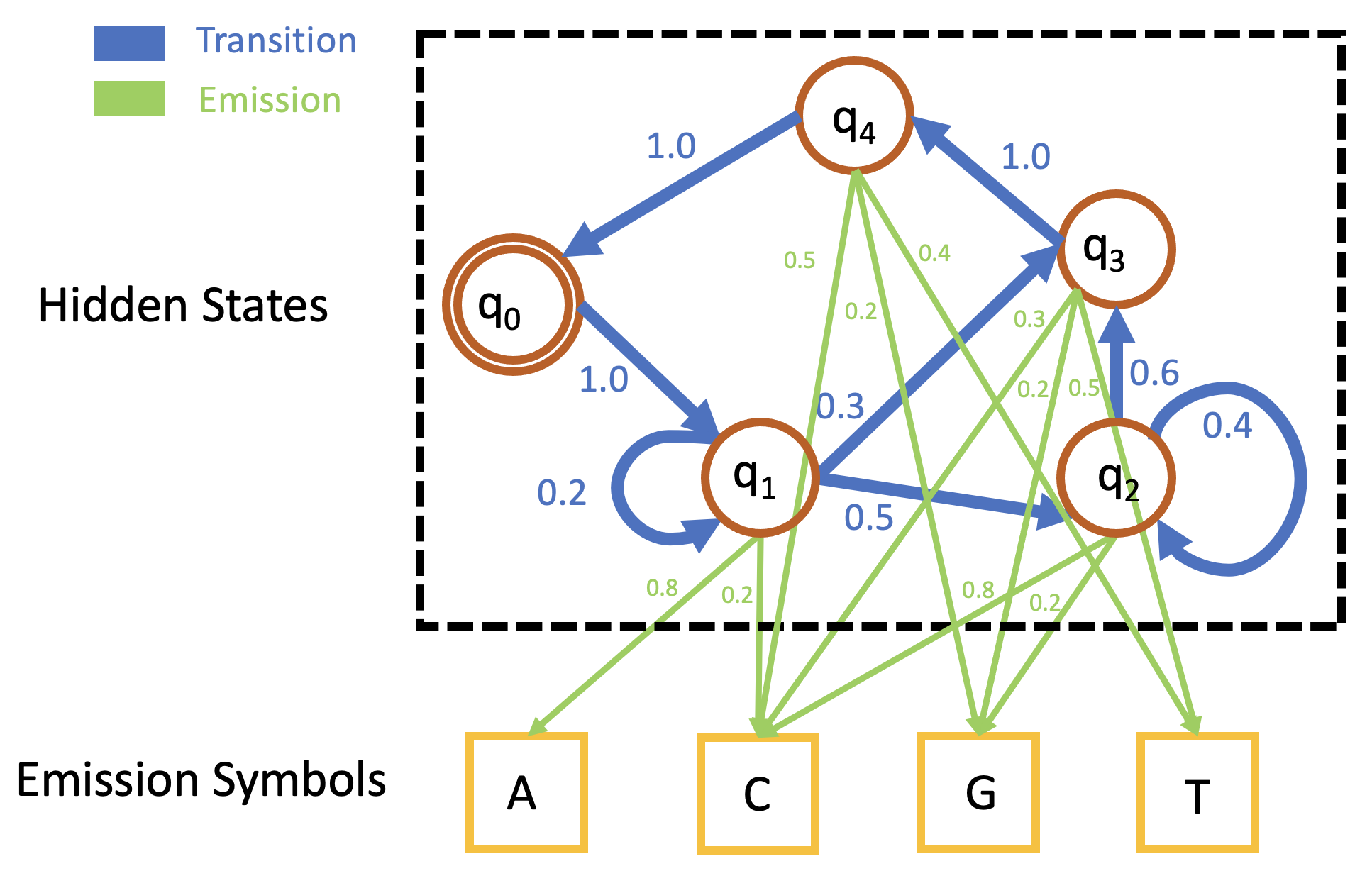
Viterbi Algorithm

Viterbi Algorithm applies dynamic programming to find the optimal path of states to maximize the probability of generating the given sequence. In detail, assume the set of all states is \[\mathcal{S} = \{q_0,q_1,\cdots,q_n\},\] the given sequence is \[L = x_0x_1\cdots x_{l-1},\] our goal is to find the path of states $P$ s.t. \[P = \underset{Q\in \text{all paths}}{\operatorname{arg max}} \,\mathbb{P}(L|Q) = \underset{Q\in \text{all paths}}{\operatorname{arg max}} \,\mathbb{P}_t(q_{0}\,|\,q_{k_{l-1}})\mathbb{P}_t(q_{k_0}\,|\,q_0)\mathbb{P}_e(x_{0}\,|\,q_{k_{0}}) \prod_{i=1}^{l-1} \mathbb{P}_t(q_{k_{i}}\,|\,q_{k_{i - 1}})\mathbb{P}_e(x_{i}\,|\,q_{k_{i}}),\] where $Q= q_{0}q_{k_0}q_{k_1}\cdots q_{k_{l-1}}q_0$. Denote the maximal probability as \[\mathbb{P}_m = \max_{Q\in \text{all paths}} \,\mathbb{P}(L|Q).\] Viterbi algorithm uses the following recursive equation to calculate $\mathbb{P}_m$ and find the path $P$ by tracing back, \[F(i,j)=\begin{cases} \displaystyle\max_{q_s\in \mathcal{S}}F(s,j-1)\mathbb{P}_t(i\,|\,q_s)\mathbb{P}_e(x_j\,|\,q_i)&1\leq j\leq l-1\\ \mathbb{P}_t(q_i\,|\,q_0)\mathbb{P}_e(x_0\,|\,q_i)&j=0\end{cases}\] where $F(i,j)$ is the function of the i-th state ($q_{i}$) and the j-th position in the sequence ($x_{j}$). Since the final step should be the transition to $q_0$, the maximal probability is \[\mathbb{P}_m(L) = \max_{q_s\in \mathcal{S}}F(s,l-1)\mathbb{P}_t(q_0\,|\,q_s).\]

Implementation

Below is the implementation of Viterbi Algorithm. 

import numpy as np
def DecodeHMM(HMM, Input_seq):
    State = list(HMM.keys())
    m = len(Input_seq) #length of seq
    n = len(State) #number of states
    
    #Initialization
    Score = [[-np.inf for x in range(n)] for x in range(m)] #scoring matrix Score[seq][state]
    Pointer =[['Null' for x in range(n)] for x in range(m)] #pointer matrix
    
    for i in range(1,n):
        PrTr = HMM[State[0]]['TR'][State[i]]
        PrEm = HMM[State[i]]['EM'][Input_seq[0]]
        Pr = np.log(PrTr)+np.log(PrEm)
        Score[0][i] = Pr
        if Pr > -np.inf : Pointer[0][i] = State[0]
    
    #Fill the score matrix and pointer matrix
    for pos in range(1,m):
        Nuc = Input_seq[pos]#nucleotide
        StateEmPos = [ i for i in State if HMM[i]['EM'][Nuc] > 0] #set of states that can emit current nucleotide
        for q in StateEmPos:
            StateTrq = [i for i in State if HMM[i]['TR'][q] > 0] #set of states that can transit to current state
            PrEm = HMM[q]['EM'][Nuc]
            for p in StateTrq:
                PrTr = HMM[p]['TR'][q]
                value = Score[pos-1][State.index(p)] + np.log(PrTr)+np.log(PrEm)
                if value > Score[pos][State.index(q)]: 
                    Score[pos][State.index(q)] = value
                    Pointer[pos][State.index(q)] = p
    #trace back
    Best = State[1] 
    Output = [State[0]]
    for i in range(2,n):
        CurrentScore = Score[m-1][i] + np.log(HMM[State[i]]['TR'][State[0]])
        MaxScore = Score[m-1][State.index(Best)] + np.log(HMM[Best]['TR'][State[0]])
        if  CurrentScore > MaxScore :
            Best = State[i]
    MaxScore = Score[m-1][State.index(Best)] + np.log(HMM[Best]['TR'][State[0]])
    Output.append(Best)

    pos = m - 1
    while pos != -1:
        Best = Pointer[pos][State.index(Best)]
        Output.append(Best)
        pos -= 1
    if MaxScore == - np.inf: 
        Output = 'Null'
    else : Output = Output[::-1]   
    return MaxScore,Output

For example, we can input a HMM and run the decoding function: 

HMM = {'q0':{'TR':{'q0':0,'q1':0.7,'q2':0.2,'q3':0, 'q4':0.1},'EM':{'A':0,'T':0,'C':0,'G':0}},
       'q1':{'TR':{'q0':0,'q1':0.2,'q2':0.3,'q3':0.5,'q4':0}, 'EM':{'A':0.45,'T':0.45,'C':0.05,'G':0.0}},
       'q2':{'TR':{'q0':0,'q1':0, 'q2':0.8,'q3':0.2,'q4':0}, 'EM':{'A':0.05,'T':0.05,'C':0.25,'G':0.65}},
       'q3':{'TR':{'q0':0,'q1':0, 'q2':0.5,'q3':0,'q4':0.5}, 'EM':{'A':0.2,'T':0.6,'C':0.1,'G':0.1}},
       'q4':{'TR':{'q0':0.3,'q1':0.2,'q2':0.5,'q3':0,'q4':0},'EM':{'A':0.4,'T':0.1,'C':0.1,'G':0.4}}}

DecodeHMM(HMM, 'ACCCT')

The output is: 

(-13.466615801344505, ['q0', 'q1', 'q2', 'q2', 'q3', 'q4', 'q0'])

Huarui Zhou @ 2023